A series of meetings designed to allow post-doc and Ph.D. students to present their research topics and promote collaborations.
On one Wednesday each month, a different research topic is presented in simple and accessible terms.
The seminars are designed to be attended by post-doc and Ph.D. students, but graduates and undergraduates are welcome.
Ph.D. courses in mathematics are coordinated by Prof. Alessandro Giuliani.
Enroll yourself or visualise the events calendar.
Next event
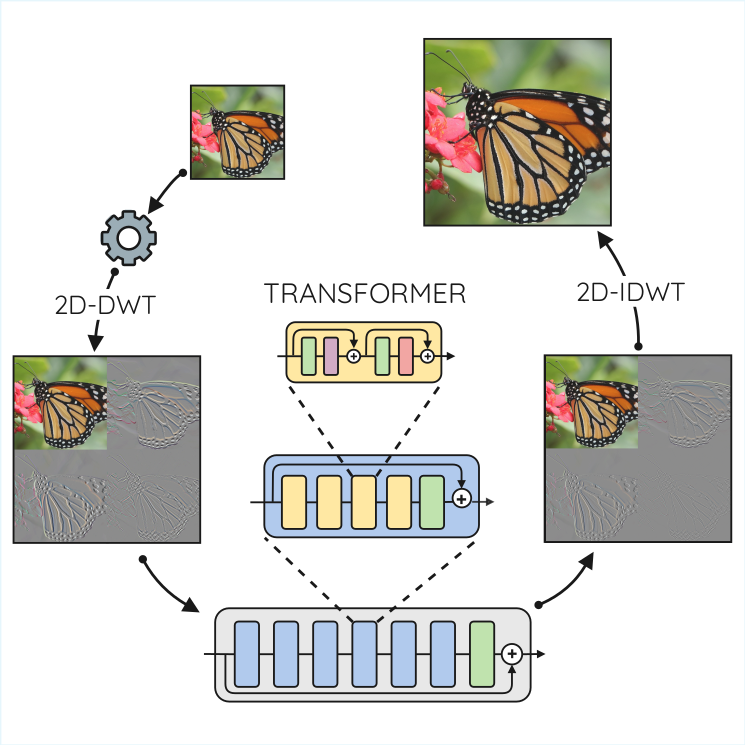
Single Image Super Resolution via Wavelets and Transformers
by Pietro Cestola
December 3, 2025 – 14:00 – Room B (Physics Dept.)
Abstract. Single Image Super Resolution (SISR) is an ill-posed problem: the lack of an intrinsic notion of “same content” across resolutions motivates its statistical formulation. We begin by clarifying this viewpoint and its relevance to our medical imaging setting. We then present an approach based on the additive refinement of the wavelet coefficients of a classically upsampled image. Building on this formulation, we introduce a super-resolution architecture that implements it by combining two-dimensional discrete wavelet transforms with the Swin Transformer. We conclude by discussing the training strategy and the use of knowledge distillation, along with quantitative and qualitative results on medical datasets.
Past events
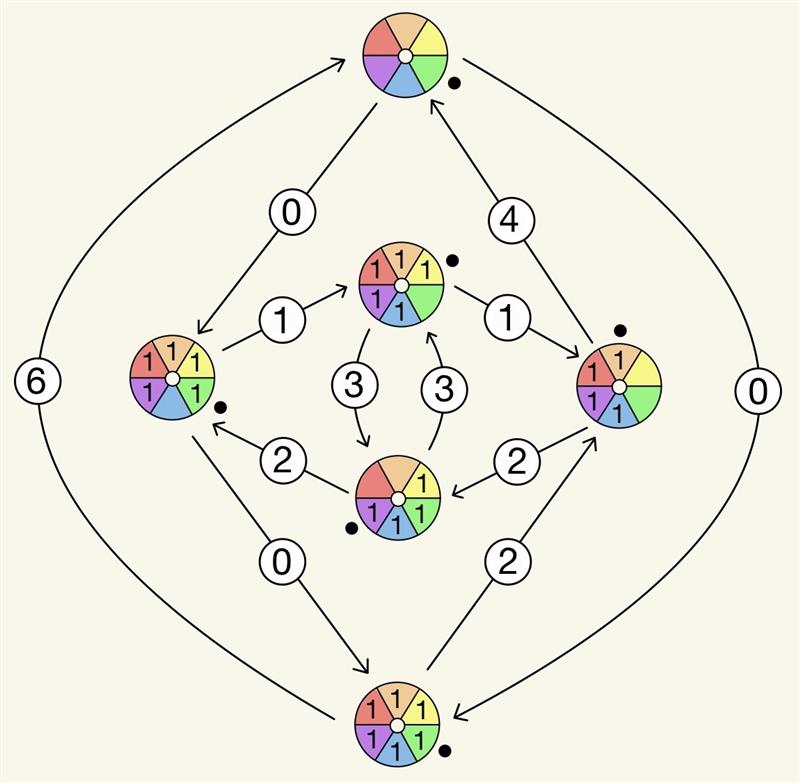
From Kauffman States to BMS States: A Framework in Combinatorics and Quiver Representation Theory
by Michele Matteucci
November 5, 2025 – 14:00 – Room B (Physics Dept.)
Abstract. Inspired by recent works exploring the interconnections between formal knot theory and quiver representation theory, we introduce new combinatorial objects generalizing the notion of a Kauffman state. A BMS state consists of a graph \(G\) embedded in an orientable surface, endowed with a nonnegative weight on the edges and a pair of integer-valued functions on the set of angles satisfying a balancing condition. Such an object is naturally associated with a representation of the Jacobian algebra of the medial quiver of \(G\). After defining two symmetric notions of partial order for BMS states, we study the structure of the category in which these objects live, in connection with the lattices of subrepresentations arising from them. Furthermore, we address questions of decomposability. Finally, we discuss polynomial aspects and outline some open problems currently under investigation.
Previous editions

Junior Seminars
Academic Year 2024/25
Partecipants.
- Wei Chen – On tangent curves
- Sara Galatro – Efficient certifying algorithms for linear classification
- Rocco Brunelli – Machine learning meets differential cryptanalysis
- Simone Marrocco – Hamiltonian methods for the Kirchhoff equation
- Mario Morellini – Nonlinear spin system
- Martina Miseri – The Prym-canonical Clifford index
- Lorenzo Baroni – Linear flow on the infinite torus

Junior Seminars
Academic Year 2023/24
Partecipants.
- Zakaria Brahimi – Cubic fourfolds: some rational examples
- Adrien Ragot – Realisability: from constructive proofs to program specification
- Muhammad Usman – 3D Human Pose Estimation: Real-time Performance and Applications
- Federico Pieroni – An overview on Coble surfaces, their moduli, and the Coble conjecture
- Luca Ferrigno – Unlikely Intersections in diophantine geometry
- Elena Sammarco – The rationality problem for the cubic fourfold

Junior Seminars
Academic Year 2022/23
Organised by
Armando Capasso and
Elia Onofri
with the participation of
Martina Miseri and
Bruno Renzi.
Partecipants.
- Armando Capasso – What is... a Higgs Bundle?
- Elia Onofri – How machine learning can improve macroscopic models for traffic state estimation and forecast
- Simone Pesatori – Coincident root loci and the moduli space of rational elliptic surfaces
- F. C. Simon Schirren – Virtual Cycles: An Introduction
- Bruno Renzi – The dimer model: phase diagram and universality
G.T.M. – General Topics in Mathematics (informal seminars)
Academic Year 2021/22
Organised by Armando Capasso and Elia Onofri
Partecipants.
- Elia Onofri – On tweakable black-box polinomials: the cube attacks family
- Armando Capasso – Numerically flatness for Higgs bundles over compact Kähler manifolds
- Luca Ferrigno – An Overview of Diophantine Geometry
- Muhammad Usman – Symbol-based preconditioning for Riesz distributed-order space-fractional diffusion equations
- Elia Onofri – Attribute-based colouring and its applications in reducing problem's size
- Armando Capasso – Algebraic hypersurfaces with vanishing Hessian and CW-complexes
- Elia Onofri – The role of the applied mathematician: optimisation of pedestrian flows in crowded museums

